SISTEM PERSAMAAN KUADRAT DAN PERSAMAAN LINEAR DUA VARIABEL BESERTA PERTIDAKSAMAANNYA

Nama : Syifa Qurrota Ayuni (34)

Kelas : X IPS 3

Tanggal : 07/09/21

Mata Pelajaran : Mat Wajib

Sistem Persamaan Kuadrat (SPK)

Sistem persamaan kuadrat dengan variabel x serta y pada umumnya dinyatakan seperti berikut ini:

y = ax² + bx + c
y = px² + qx + r

Keterangan:

Dengan a, b, p, q, r merupakan bilangan real.

Cara Penyelesaian SPK

1. Substitusikan persamaan yang satu ke dalam persamaan yang lainnya sehingga akan membentuk persamaan kuadrat.
2. Menentukan akar-akar persamaan kuadrat yang terbentuk sehingga akan kita dapatkan himpunan penyelesaiannya, yaitu: {(x1,y1),(x2,y2)}

Contoh Soal :

Himpunan penyelesaian dari sistem persamaan di bawah ini adalah....

Jawab:

Substitusikan persamaan dari y = x² -2x – 3 ke dalam persamaan y = -x² -2x + 5, sehingga:

x² -2x – 3 = -x² -2x + 5
<=> 2x² -8 = 0
<=> x² – 4 = 0
<=> (x – 2)(x + 2) = 0
<=> x = 2 atau x = -2

Untuk x = 2
y = x² – 2x – 3
y = (2)² -2 (2) – 3
y = 4 – 4 – 3
y = -3

Untuk x = -2
y = x² – 2x – 3
y = (-2)² -2 (-2) – 3
y = 4 + 4 – 3
y = 5

Maka dari itu, himpunan penyelesaiannya dari soal di atas adalah {(-2,5),(2,-3)}

Sistem persamaan linear dua variabel (SPLDV)

adalah pasangan dari dua nilai peubah x atau y yang ekuivalen dengan bentuk umumnya yang mempunyai pasangan terurut (xo, yo). Bentuk umum dari SPLDV adalah sebagai berikut : 

ax + by = p

cx + dy = q

Contoh Soal :

Carilah himpunan penyelesaian dari SPLDV berikut ini : 

3x + 2y = 10

9x – 7y = 43

Penyelesaian : 

Langkah 1 : nyatakan ke dalam variabel y

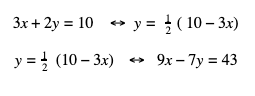
Langkah 2 : selesaikan nilai x dan y

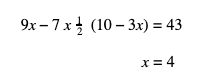
Langkah 3 : substitusikan nilai x dan y ke dalam persamaan : 

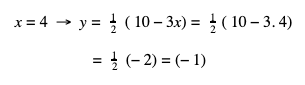
Jadi, Himpunan penyelesaiannya adalah {4, -1}.

Sistem pertidaksamaan linear dua variabel (SPtLDV) 

adalah bentuk pertidaksamaan yang memuat dua peubah (variabel) dengan pangkat tertinggi variabel tersebut adalah satu.

Bentuk dari pertidaksamaan linear dua variabel yaitu sebagai berikut.

Bentuk Umum Pertidaksamaan Linear 2 Variabel

ax + by > c

ax + by < c

ax + by ≥ c

ax + by ≤ c

Keterangan:

• x, y : variabel
• a  : koefisien variabel x
• b  : koefisien variabel y
• c   : konstanta
• <, >, ≤, ≥  : tanda pertidaksamaan

Contoh Soal :

3x + 2y < 8

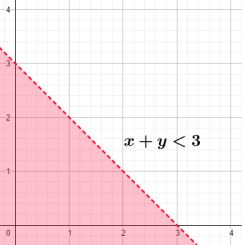
x + y < 3

Tentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel tersebut jika x dan y merupakan bilangan bulat positif.

Pembahasan :

3x + 2y < 8

x + y < 3

Dengan menggunakan grafik, dibuat garis 3x + 2y = 8, kemudian tentukan bagian yang merupakan 3x + 2y < 8.

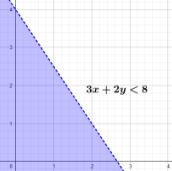
Dengan menggunakan grafik, dibuat garis x + y = 3, kemudian tentukan bagian yang merupakan x + y < 3.

Kemudian tentukan titik potong kedua garis tersebut.

3x + 2y = 8

x + y = 3

Dengan menggunakan metode eliminasi diperoleh:

3x + 2y = 8

2x + 2y = 6

————– –

x   = 2

Substitusikan nilai x = 2 ke persamaan x + y = 3

2 + y = 3

y = 3 – 2

y = 1

Titik potong kedua garis tersebut adalah (2, 1).

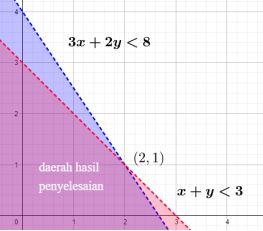
Daerah berwarna ungu merupakan daerah hasil penyelesaian sistem pertidaksamaan linear dua variabel.

Daftar Pustaka : 

1. https://www.yuksinau.id/sistem-persamaan-linier-kuadrat-dua-variabel/

2. https://www.quipper.com/id/blog/mapel/matematika/persamaan-linear-dua-variabel-matematika-kelas-10/

3. https://rumuspintar.com/pertidaksamaan-linear/#:~:text=Pertidaksamaan%20linear%20dua%20variabel%20adalah,dua%20variabel%20yaitu%20sebagai%20berikut.&text=Keterangan%3A,-x%2C%20y%20%3A%20variabel&text=%2C%20%E2%89%A4%2C%20%E2%89%A5%20%3A%20tanda%20pertidaksamaan,-Selanjutnya%20akan%20dibahas