FUNGSI: KUADRAT, RASIONAL, IRASIONAL
Fungsi kuadrat adalah sebuah fungsi polinom yang memiliki peubah/variabel dengan pangkat tertingginya adalah 2 (dua).
Secara umum fungsi kuadrat memiliki bentuk umum seperti berikut ini:
f(x) = ax2 + bx + c, a ≠ 0
dengan f(x) = y yang merupakan variabel terikat, x adalah variabel bebas, sedangkan a, dan b merupakan koefisien dan c adalah suatu konstanta.
Jenis-jenis lain dari fungsi kuadrat seperti di bawah ini:
1. Jika pada y = ax2 + bx + c nilai b dan c adalah 0, maka fungsi kuadrat menjadi:
y = ax2
yang membuat grafik pada fungsi ini simetris pada x = 0 dan memiliki nilai puncak di titik (0,0)
2. Jika pada y = ax2 + bx + c nilai b bernilai 0, maka fungsi kuadrat akan berbentuk:
y = ax2 + c
yang membuat grafik pada fungsi ini simetris pada x = 0 dan memiliki titik puncak di (0,c)
3. Jika titik puncak ada di titik (h,k), maka fungsi kuadrat menjadi:
y = a(x – h)2 + k
dengan hubungan a, b, dan c dengan h, k adalah sebagai berikut:
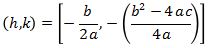
Tentukan nilai maksimum dari fungsi y = x2 – x – 6.
Nilai maksimum dari suatu fungsi kuadrat adalah
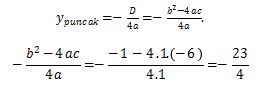
Jadi, ypuncak = – 23/4
Fungsi Rasional :
Fungsi rasional merupakan fungsi yang mempunyai bentuk umum
Dengan p dan d adalah polinomial dan d(x) ≠ 0. Domain dari V(x) merupakan seluruh bilangan real, kecuali pembuat nol dari d.
Adapun fungsi rasional yang paling sederhana, yakni fungsi y = 1/x dan fungsi y = 1/x².
Di mana keduanya mempunyai pembilang konstanta sertaa penyebut polinomial dengan satu suku. Dan kedua fungsi tersebut mempunyai domain semua bilangan real kecuali x ≠ 0.
Contoh Soal Fungsi Rasional :
Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional
Untuk y = 1/x dalam kuadran III,
- Mendeskripsikan sifat dari ujung grafik fungsi tersebut.
- Mendeskripsikan apa yang akan terjadi pada saat x mendekati nol.
Pembahasan Serupa dengan sifat grafiknya pada kuadran I, maka akan kita peroleh
- Pada saat x mendekati negatif tak hingga, nilai y akan mendekati nol. Jika disimbolkan akan menjadi: x → –∞, y → 0.
- Pada saat x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga bisa kita tuliskan dengan simbol x → 0–, y → –∞.
Fungsi y = 1/x²
Dari pembahasan di atas, kita bisa mengetahui bahwa grafik dari fungsi ini akan mengalami jeda pada saat x = 0.
Namun demikian, sebab kuadrat dari sembarang bilangan negatif merupakan bilangan positif, cabang-cabang dari grafik fungsi ini akan terletak kdi atas sumbu-x.
Perhatikan bahwa fungsi y = 1/x² adalah fungsi genap.

Sama halnya dengan y = 1/x, nilai x yang mendekati positif tak hingga akan menghasilkan y yang mendekati nol. Jika kita tulis simbolnya maka akan menjadi: x → ∞, y → 0.
Hal ini adalah salah satu indikasi dari sifat asimtot dalam arah horizontal. Serta kita akan menyatakan y = 0 adalah asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,
Asimtot Horizontal
Diberikan sebuah konstanta k, garis y = k adalah asimtot horizontal dari fungsi V(x) apabila x bertambah tanpa batas, akan menimbulkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.
Pada gambar (a) di bawah ini menggambarkan garis asimtot horizontal pada y = 1, yang menunjukan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan.
Gambar (b) menggambarkan garis asimtot horizontal pada y = –2, yang menunjukan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.

Fungsi Irasional :
Fungsi irrasional adalah fungsi yang memetakan himpunan bilangan real tak negatif kepada himpunan itu sendiri. Sehingga fungsi irrasional memiliki syarat bahwa fungsi akan terdefinisi apabila nilai di dalam akar tersebut tidak negatif.
Contoh Soal Fungsi Irrasional :
1. Selesaikanlah Persamaan irasional,

Daftar Pustaka : Fungsi Kuadrat Fungsi Rasional Fungsi Irrasional (01) Fungsi Irrasional (02)




